Pour symboliser une valeur qui varie dans le temps, nous utilisons les mathématiques et le tracé de courbes suivant deux axes, x et y. L’axe horizontal des x représente le temps, l’axe vertical des y représente la valeur qui fluctue en fonction du temps. La croissance économique est une valeur qui représente la production de richesses et évolue dans le temps en constante augmentation comme son nom l’indique. Il y a en gros deux sortes de progressions, l’une qui varie d’une certaine quantité absolue pour un certain laps de temps, l’autre qui varie d’une certaine quantité relative par rapport à la valeur globale.
Progression arithmétique
Soit un artisan qui fabrique des chaises. Il a un stock de 20 chaises et en fabrique 1 par jour. Son stock augmente donc de 1 chaise par jour, c’est une suite arithmétique.
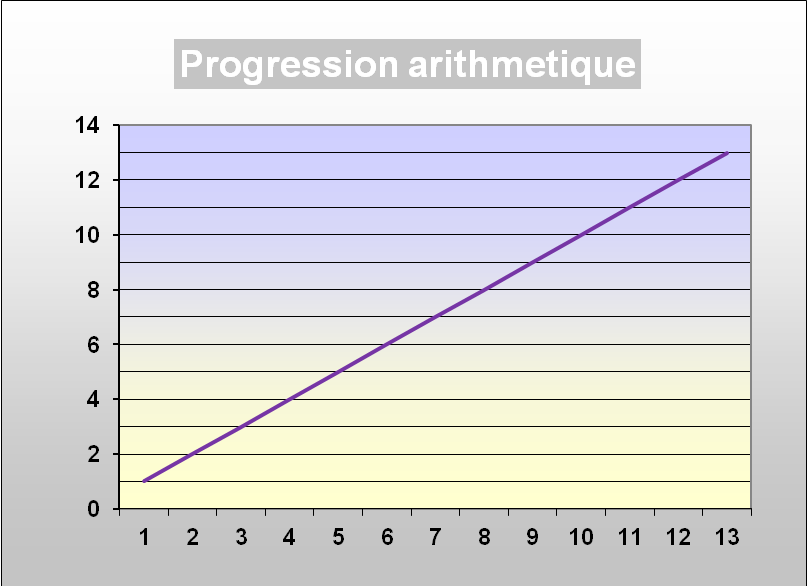
La variation est absolue, 1 chaise par jour. La production par jour n’est pas liée à la taille du stock.
La valeur précédente est augmentée d’une certaine valeur.
Progression géométrique
Soit un arbre dont le tronc principal produit 2 bourgeons en 1 semaine. Ces bourgeons poussent et produisent à nouveau chacun 2 bourgeons en 1 semaine. Le nombre de ramifications double chaque semaine. C’est une suite géométrique.
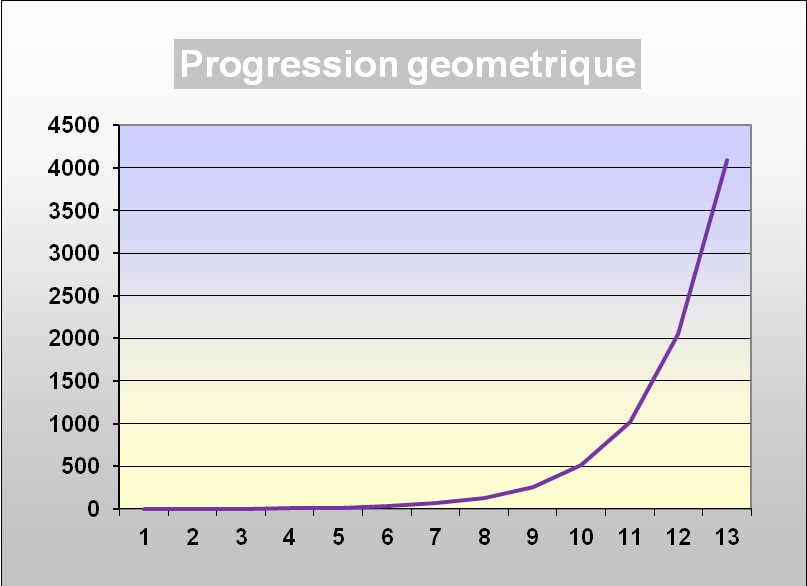
Le nombre de ramifications est relatif au nombre de ramifications passées. La variation est fonction de la valeur précédente, la progression est exponentielle.
La valeur précédente est multipliée par une certaine valeur.
Croissance exponentielle
Ce qui caractérise la croissance exponentielle est donc le fait que la valeur précédente est multipliée par une certaine valeur. La formule générale est la suivante :
T (nombre d’années) = log (multiplicateur) / log (1+intérêt annuel)
Ce qui est classique est d’étudier le doublement, chaque fois qu’une valeur est multipliée par deux. Pour une progression annuelle de 5%, nous aurons donc un temps de doublement de :
log(2) / log(1+0,05) = 14,2 ans
Nous avons tous appris à l’école l’histoire du sultan proposant à l’inventeur de l’échiquier de le remercier en grains de blé. Un sur la première case, deux sur la deuxième, quatre sur la troisième et ainsi de suite. Pour couvrir l’échiquier (64 cases), il faudrait environ 1500 ans de production actuelle.
Ce qui est possible en mathématique ne l’est pas obligatoirement en physique terrestre.
La croissance économique se heurte à la réalité physique des ressources naturelles finies et à la surface finie du globe terrestre.
Courbe en cloche
Dans la réalité physique terrestre, toute production de ressource naturelle finie, mines, carrières, puits de pétrole ou d’exploitation de ressource naturelle renouvelable en déplétion, foret, pèche, est toujours une courbe en cloche.
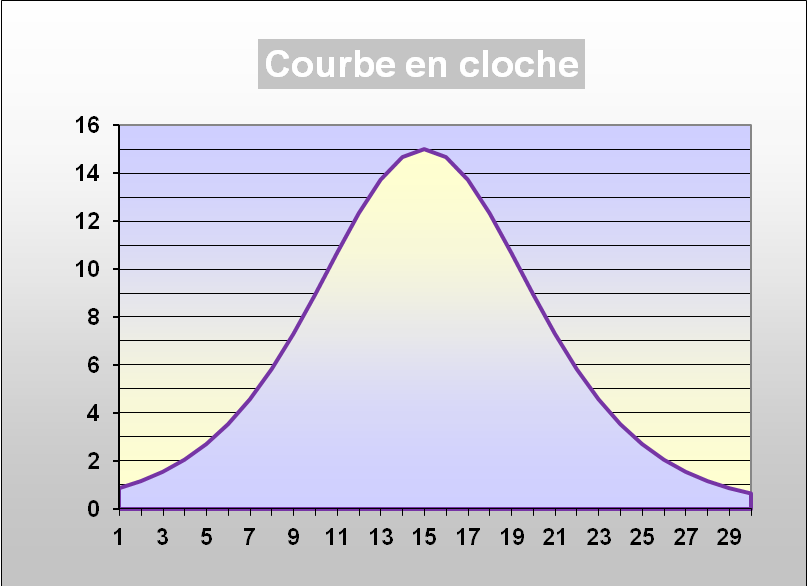
La production démarre lentement, progresse de façon exponentielle, puis la croissance de la production ralentit, la production atteint un maximum et commence à décliner. La croissance devient la décroissance. La surface sous la courbe représente la production totale, c’est-à-dire les réserves de la ressource naturelle concernée.
De plus, pour ce qui concerne l’exploitation des combustibles fossiles et des minerais, nous avons exploité d’abord le plus facile, il ne nous reste donc maintenant que le plus difficile. La courbe ne sera donc pas symétrique, la descente sera plus rapide que la montée.
Conclusion
Il est grand temps que le monde économique reconnaisse que la croissance exponentielle n’est guère possible en physique terrestre et prenne en compte le caractère fini de certaines ressources naturelles dont l’exploitation ne sera autre qu’une courbe en cloche.
